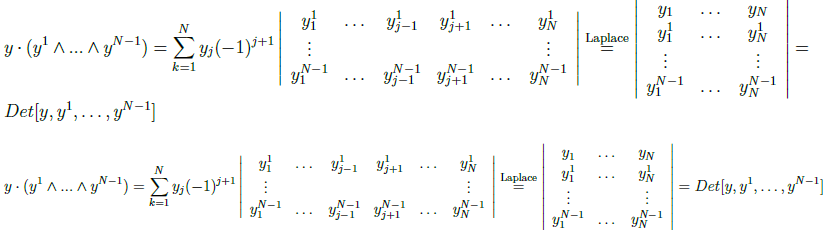$\displaystyle y \cdot (yˆ1 \wedge ... \wedge yˆ{N-1}) = \sum_{k=1}ˆN y_j(-1)ˆ{j+1} \left| \begin{array}{cccccc} yˆ1_1 & \dots & yˆ1_{j-1} & yˆ1_{j+1} & \dots & yˆ1_N \\ \vdots & & & & & \vdots \\ yˆ{N-1}_1 & \dots & yˆ{N-1}_{j-1} & yˆ{N-1}_{j+1} & \dots & yˆ{N-1}_N \end{array} \right| \stackrel{\text{Laplace}}{=} \left| \begin{array}{ccc} y_1 & \dots & y_N \\ yˆ1_1 & \dots & yˆ1_N \\ \vdots & & \vdots \\ yˆ{N-1}_1 & \dots & yˆ{N-1}_N \end{array} \right|=Det[y,yˆ1,\dots,yˆ{N-1}]$

\scalebox{0.85}{$\displaystyle y \cdot (yˆ1 \wedge ... \wedge yˆ{N-1}) = \sum_{k=1}ˆN y_j(-1)ˆ{j+1} \left| \begin{array}{cccccc} yˆ1_1 & \dots & yˆ1_{j-1} & yˆ1_{j+1} & \dots & yˆ1_N \\ \vdots & & & & & \vdots \\ yˆ{N-1}_1 & \dots & yˆ{N-1}_{j-1} & yˆ{N-1}_{j+1} & \dots & yˆ{N-1}_N \end{array} \right| \stackrel{\text{Laplace}}{=} \left| \begin{array}{ccc} y_1 & \dots & y_N \\ yˆ1_1 & \dots & yˆ1_N \\ \vdots & & \vdots \\ yˆ{N-1}_1 & \dots & yˆ{N-1}_N \end{array} \right|=Det[y,yˆ1,\dots,yˆ{N-1}]$}